Single and Continuous-Span Beam Analysis worksheet

Single and Continuous-Span Beam Analysis
Program Description:
“BEAMANAL” is a spreadsheet program written in MS-Excel for the purpose of analysis of either single-span or continuous-span beams subjected to virtually any type of loading configuration. Four (4) types of single-span beams and two (2) through (5) span, continuous-span beams, considered. Specifically, beam end reactions as well as the maximum moments and deflections are calculated. Plots of all of the diagrams are produced, as well as a tabulation of the shear, moment, slope, and deflection for the beam or each individual span. Also, for structural steel single-span beams an AISC 9th Edition (ASD) Code check can be performed for X-axis bending and shear.
This program is a workbook consisting of four (4) worksheets, described as follows:
Worksheet Name Description
Doc This documentation sheet
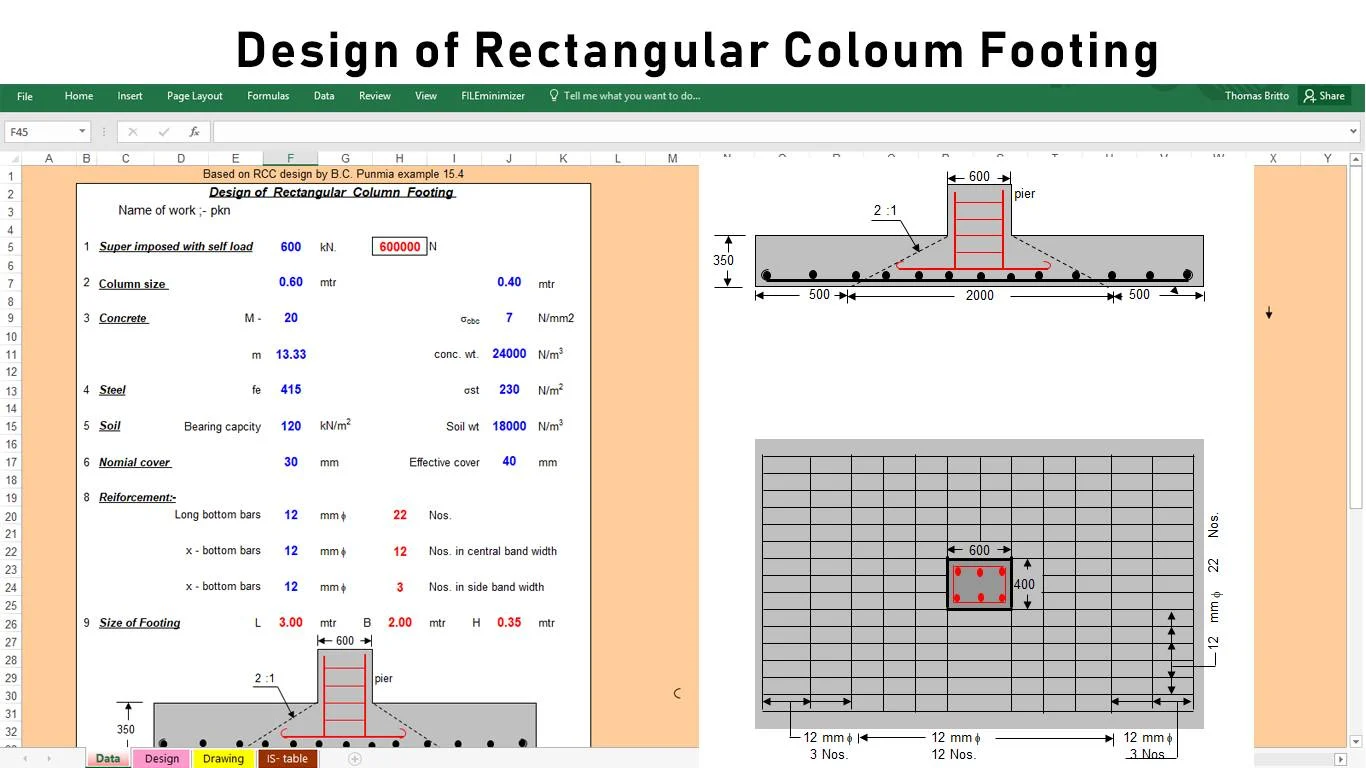
Single-Span Beam Single-span beam analysis for simple, propped, fixed, & cantilever beams
Single-Span Beam & Code Check Single-span beam analysis and AISC 9th Ed. Code Check for X-axis bending
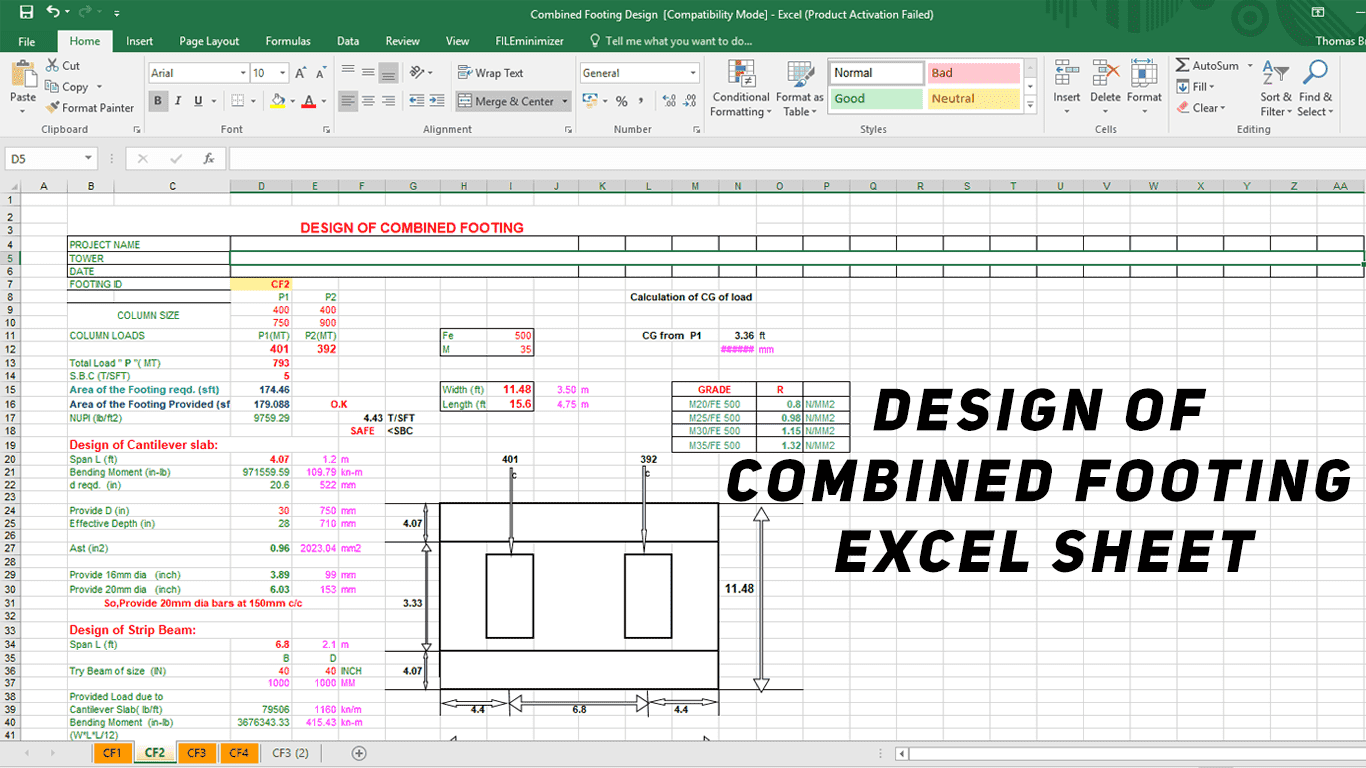
Continuous-Span Beam Continuous-span beam analysis for 2 through 5 span beams
Program Assumptions and Limitations:
1. The following reference was used in the development of this program (see below):
“Modern Formulas for Statics and Dynamics, A Stress-and-Strain Approach” by Walter D. Pilkey and Pin Yu Chang, McGraw-Hill Book Company (1978), pages 11 to 21.
2. This program uses the three (3) following assumptions as a basis for analysis:
a. Beams must be of constant cross section (E and I are constant for entire span length).
b. Deflections must not significantly alter the geometry of the problem.
c. Stress must remain within the “elastic” region.
3. On the beam or each individual span, this program will handle a full length uniform load and up to eight (8) partial uniform, triangular, or trapezoidal loads, up to fifteen (15) point loads, and up to four (4) applied moments.
4. For single-span beams, this program always assumes a particular orientation for two (2) of the the four (4) different types. Specifically, the fixed end of either a “propped” or “cantilever” beam is always assumed to be on the right end of the beam.
5. This program will calculate the beam end vertical reactions and moment reactions (if applicable), the maximum positive moment and negative moment (if applicable), and the maximum negative deflection and positive deflection (if applicable). The calculated values for the end reactions and maximum moments and deflections are determined from dividing the beam into fifty (50) equal segments with fifty-one (51) points,
and including all of the point load and applied moment locations as well. (Note: the actual point of maximum moment occurs where the shear = 0, or passes through zero, while the actual point of maximum deflection is where the slope = 0.)
6. The user is given the ability to input two (2) specific locations from the left end of the beam to calculate the shear, moment, slope, and deflection.
7. The user is also given the ability to select an AISC W, S, C, MC, or HSS (rectangular tube) shape to aide in obtaining the X-axis moment of inertia for input for the purely analysis worksheets.
8. The plots of the shear and moment diagrams as well as the displayed tabulation of shear, moment, slope, and deflection are based on the beam (or each individual span) being divided up into fifty (50) equal segments with fifty-one (51) points.
9. For continuous-span beam of from two (2) through five (5) spans, this program utilizes the “Three-Moment Equation Theory” and solves a system simultaneous equations to determine the support moments
10. This program contains numerous “comment boxes” which contain a wide variety of information including explanations of input or output items, equations used, data tables, etc. (Note: presence of a “comment box” is denoted by a “red triangle” in the upper right-hand corner of a cell. Merely move the mouse pointer to the desired cell to view the contents of that particular “comment box”.)
Click Here to Download